Tag System - kolja

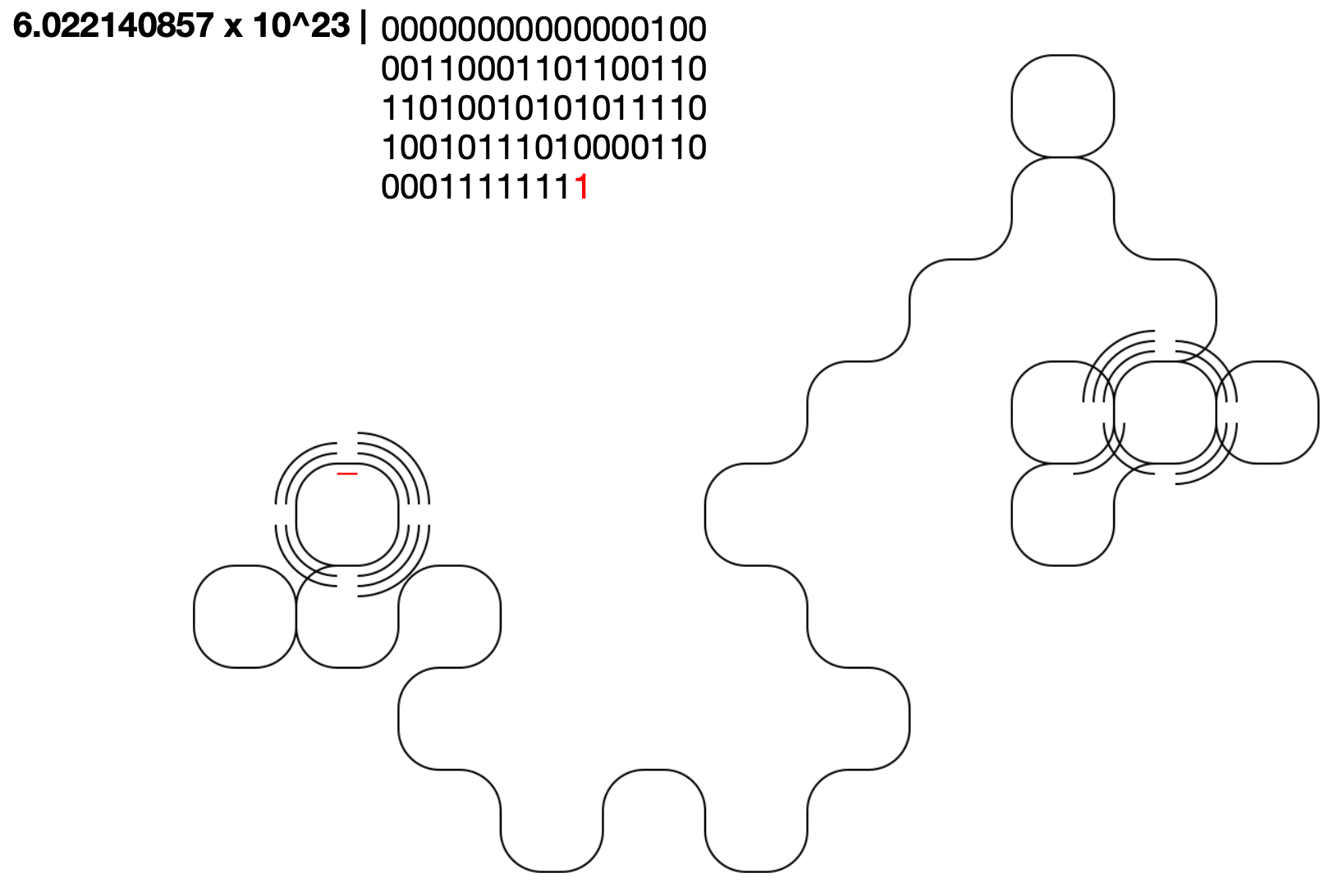
The tag system evolved from an exploration of product tag concepts. It allows to uniquely tag a product with its serial tag in the form of a symbol instead of a number. The tag system is a two-way street; any given number can be encoded as a tag figure and each tag figure can be translated back to a number. The system is based on the information content of the binary number system, describing any real number with 0’s and 1’s. The resulting sequence of bits is used to visually create a sequence of curves, where the bit information is stored in the direction of the curve. A 0 is represented by a 90 degree curve to the right, whereas a 1 is expressed as 90 degree curve to the left.

c u r v e_{i} = {\begin{array}{cl} r i g h t c u r v e, \\ l e f t c u r v e, \end{array}

Due to the nature of the binary system, the number of curves within the tags increase quite rapidly, especially for numbers in the range of $[0, 100]$ . The size of the tag itself provides an intuition for the encoded number. These properties make the tag system especially suited for tags of limited product lines, which periodically start back at zero.

Computation

The computation of the tag figure given a number can be summarized in two steps:

convert number to binary number system
apply curve rule to the sequence and draw figure

The computed tags and the corresponding binary sequence for the numbers 0-9 are visualized in the figure below, with the start of the figure being marked with a red underscore.

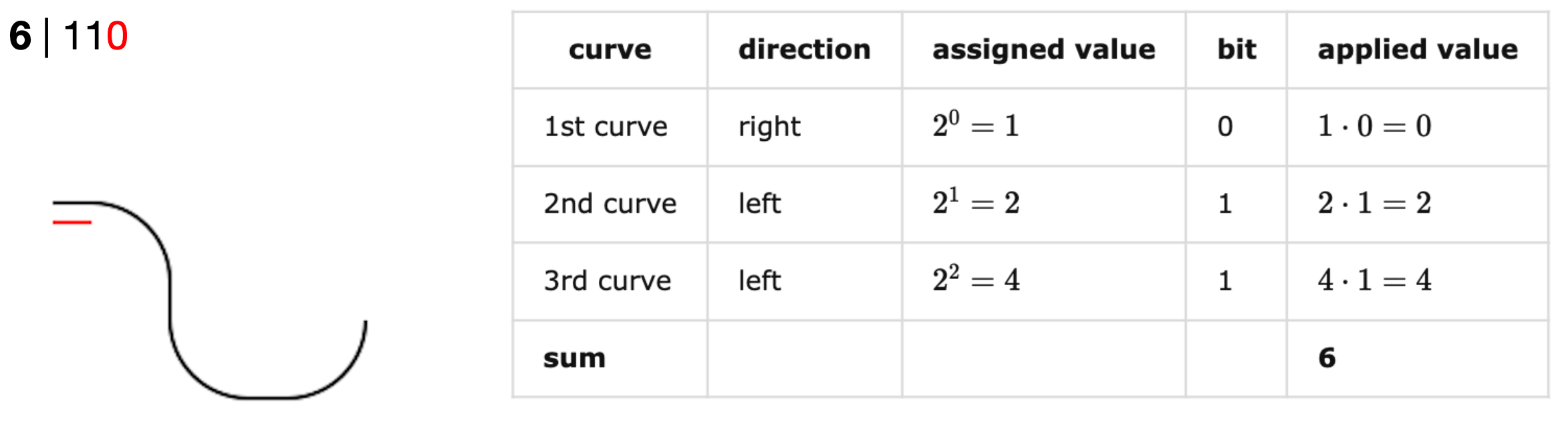
In order to assign consistent values to each curve, the transformed binary number is processed from right to left. Therefore, the first curve that is drawn in the figure represents the last bit of the binary sequence. The assigned curve value is explicitly expressed as

c u r v e v a l u e_{i} = 2^{i - 1} .

In order to reverse-engineer the encoded number given a tag figure, the curve values are multiplied by the value of the current bit, 0 or 1, which are given by the direction of the current curve. The sum of these applied values equals the encoded number. Explicitly, the formula for the number calculation is defined as

number =

The procedure is demonstrated with the example of the tag figure of number 6.

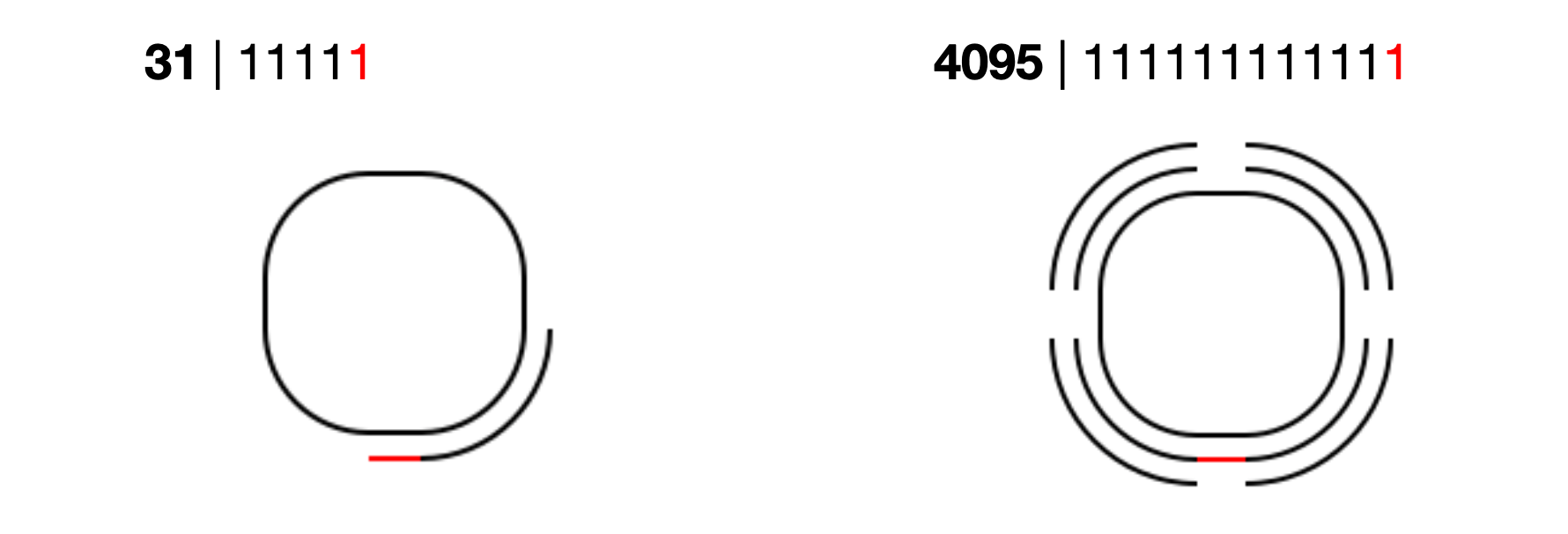
It is possible for the tag figure to pass through the same curve multiple times. In order to visualize these instances, the curve is drawn with an offset that is multiplied by the number of times it has already passed this particular sequence.

The computation process of the tag system has been automated with a python script. The code outputs the tag figure as a png and svg file, allowing a seamless implementation in most production processes.

Further Examples

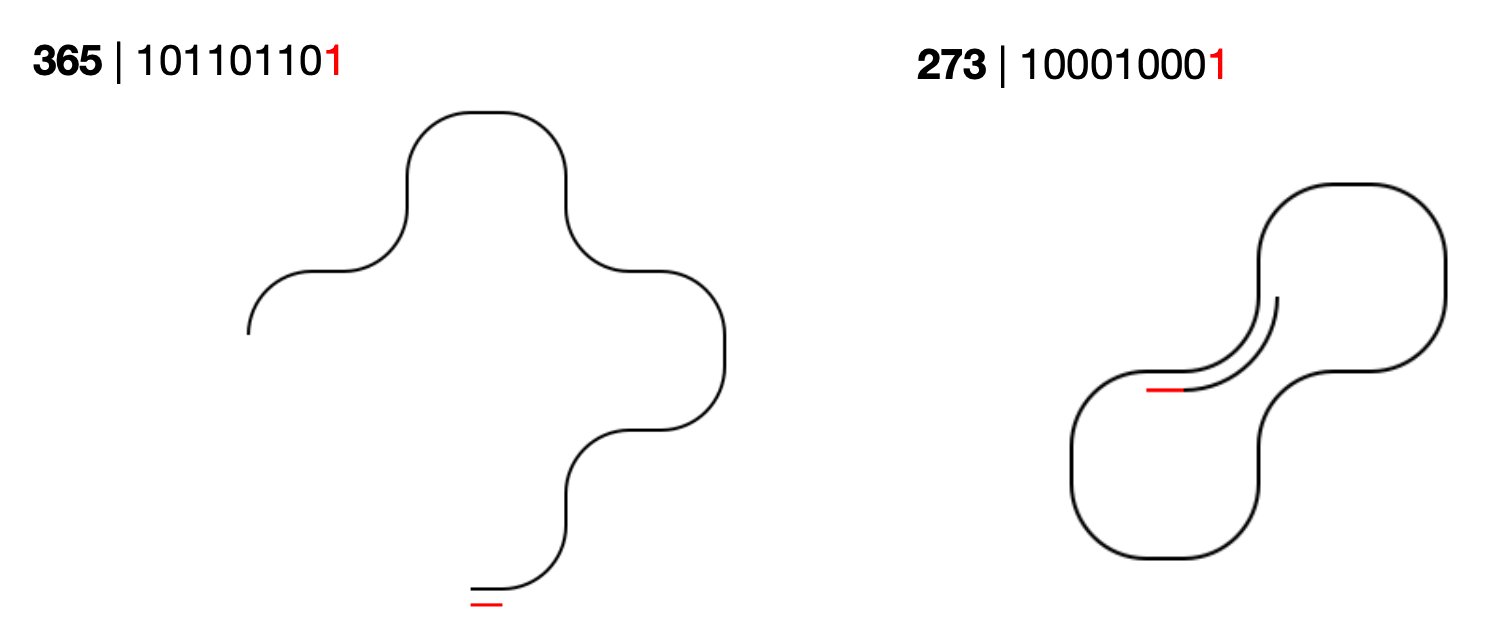
To provide some intuition of the tag system, two more examples are presented with numbers in the range of $[100, 1000]$ . The graphic below shows the tag figure of 365, the number of days in a year (left), and 273, the rounded absolute zero in Kelvin (right).

The final example is all about pushing the boundaries of the tag system. Although it is highly irrelevant for any product tag, the graphic below shows the resulting tag figure of Avogadro’s constant, $6.022 \cdot 1 0^{23}$ .