
Designers and engineers are often confronted with problems that involve a large number of parameters, contradicting objectives and a set of various constraints. Finding solutions in this high-dimensional setting that need to live up to certain performance requirements is a time-consuming procedure.
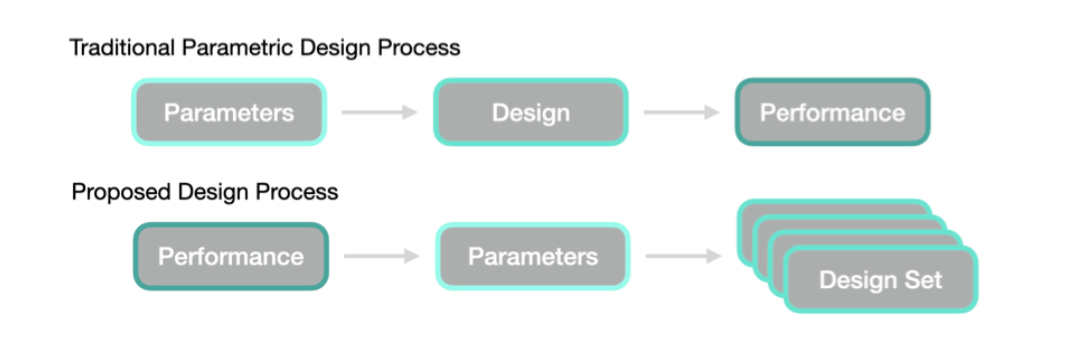
In this thesis, a deep learning concept is proposed which enables the reversal of the traditional process by learning the underlying relationship of input parameters and performance attributes. This empowers the user to request a set of attributes and generate various design instances meeting those requirements. The model augments the users ability to efficiently explore the solution space of the given design problem.
In order to achieve this objective, a Conditional Variational Autoencoder, or CVAE, is employed. A CVAE model consists of two neural networks, an encoder and a decoder. The encoder compresses the input into the latent space vector z, while the decoder expands this vector to the output. The model is trained to produce outputs that are accurate reconstructions of the original inputs, while only seeing the low-dimensional latent vector. A full forward pass of the CVAE is formulated as:
output=decoder(encoder(input)).
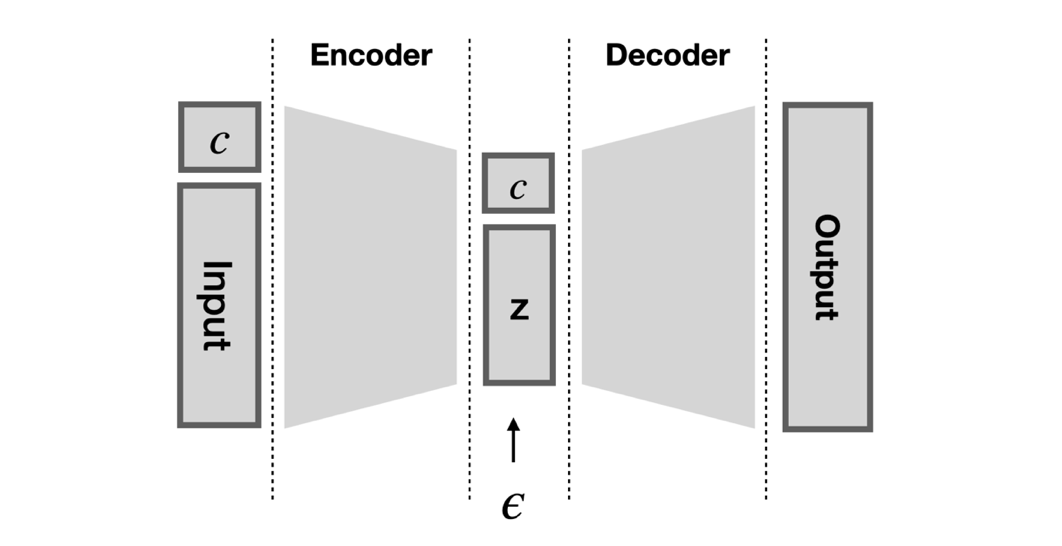
zε=μ+σ∗ϵ,∼N(0,1),
where μ and σ are the outputs of the encoder network. The loss function of the CVAE is typically formulated as the evidence lower bound, or ELBO, and consists of the reconstruction error and the KL divergence of the latent space and its prior. The ELBO is formally defined as:
ELBO=min(Eq[logq(z∣w,x)−logp(z)]−Eq[logp(w∣z,x)]),
where q represents the encoder, p the decoder, w the input and x the conditionality.
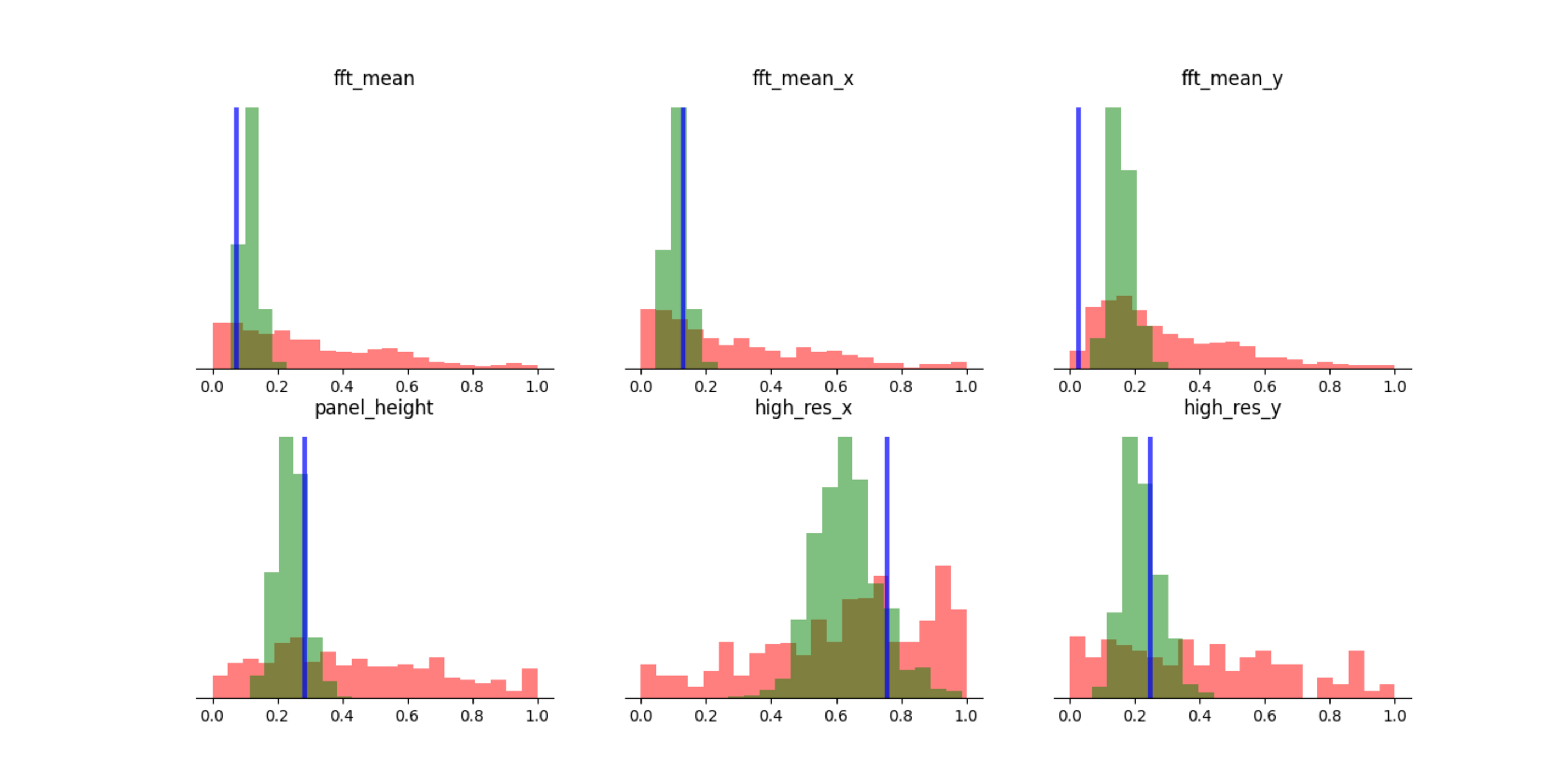
In this case study, the model is tested on its ability to generate acoustic panels that are conditioned on a set of performance attributes. An acoustic panel landscape is generated by sampling designs from the latent space of the trained CVAE model, where the conditionality is set equal to the requested attributes. The panel landscape is the models representation of the conditional acoustic panel solution space.

The landscape is evaluated by plotting the performance attribute distribution of the generated panels in green, the training data distribution in red and displaying the requested attribute value as a blue line.
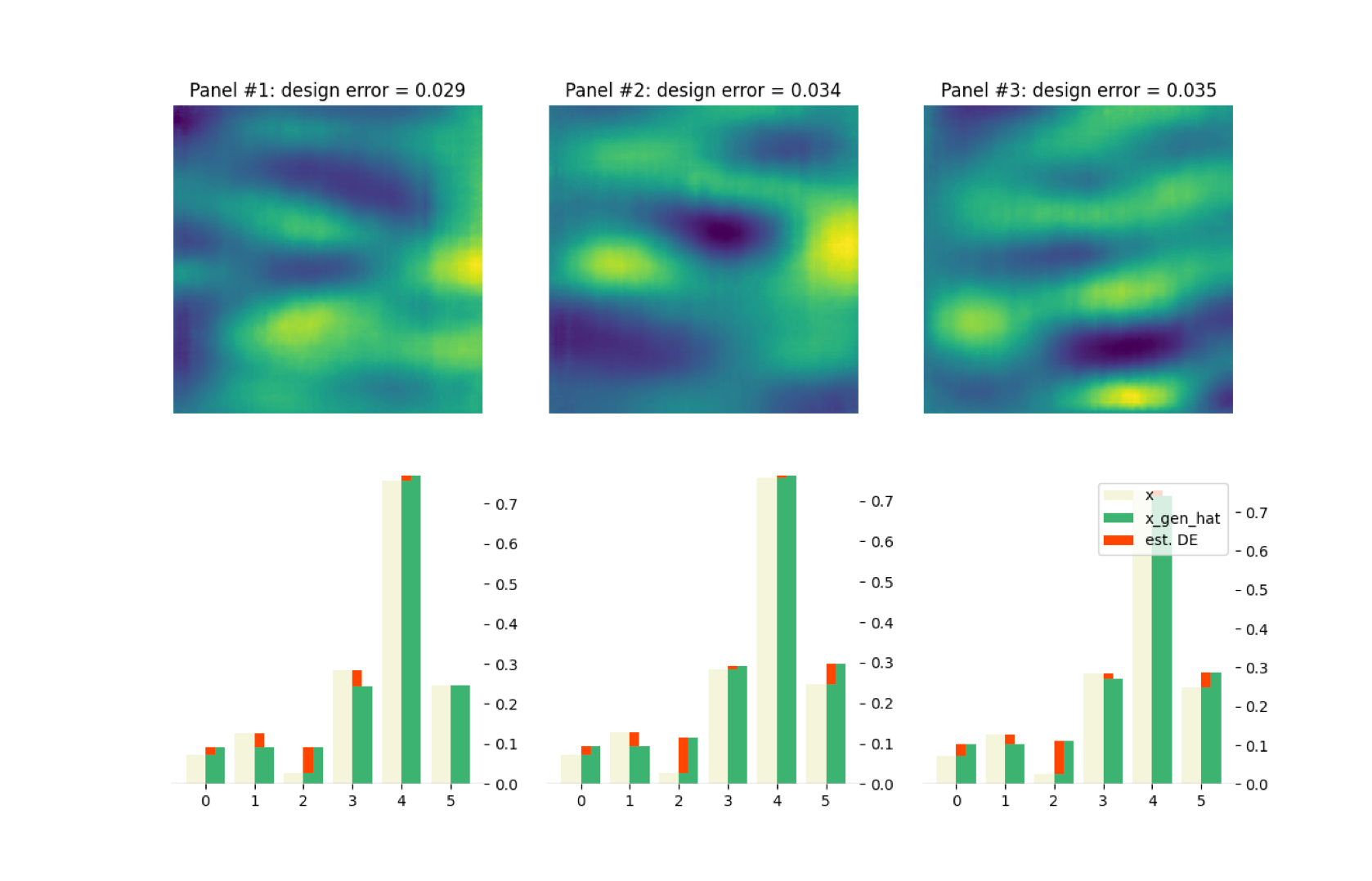
After evaluating the attribute distributions, a selection of the three best performing acoustic panels is made and the corresponding attribute errors are shown. Initially, the acoustic panels are generated as 2d heatmaps. The accumulation of the attribute errors give the design error, which is equal to 0.029 for the best performing panel. This yields a relative design error of 2.9% or a design accuracy of 97.1%.
Lastly, the heatmaps of the selected panels are modeled in a 3d environment. Although they do have similar properties to one another, the hills and valleys within the topologies are uniquely arranged, solving the problem statement of conditioned solution space exploration for acoustic panels.

For a more detailed presentation of this thesis, see the full report.
 Free Form
Free Form