Parametric Modeling: Double-Helix Masonry Domes

Background

In the 15th century, sculptor and architect Filippo Brunelleschi developed an ingenious system that was employed for the construction of the worlds largest masonry dome, the Santa Maria del Fiore in Florence. The secret of its stability lies in the arrangement of its bricks, also called the double-helix of masonry.

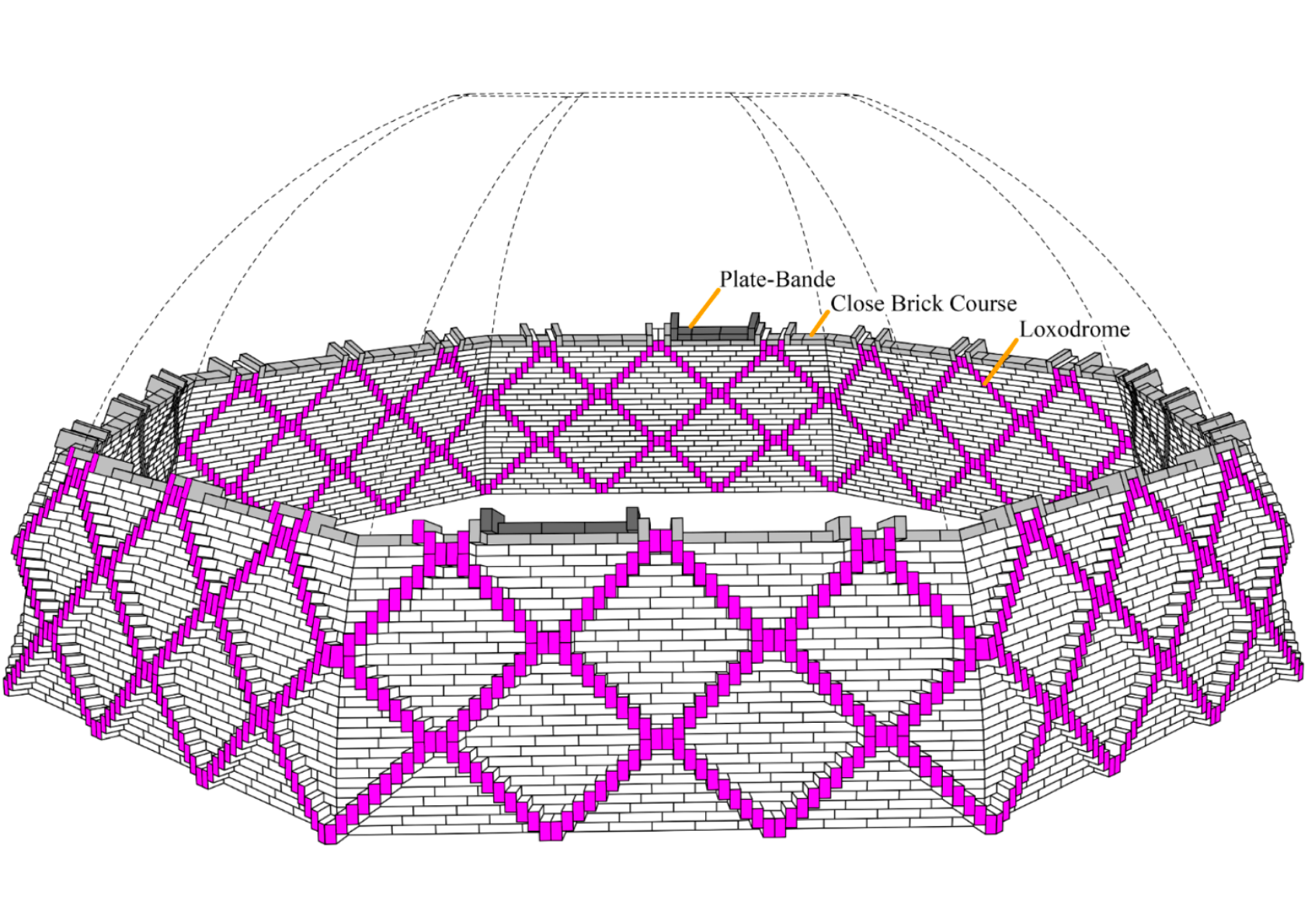
One of the main characteristics of the ingenious double-helix pattern is that it allows to perform the construction of a dome without the use of scaffolds or flying buttresses, as it is self-supporting at each step during construction. In this thesis, the completed double-helix masonry dome is analyzed on its structural properties and the internal forces are computed by solving for its rigid body equilibrium (RBE). An extensive understanding of the pattern’s influence on the transmission of forces is built up throughout the thesis.

Parametric Model

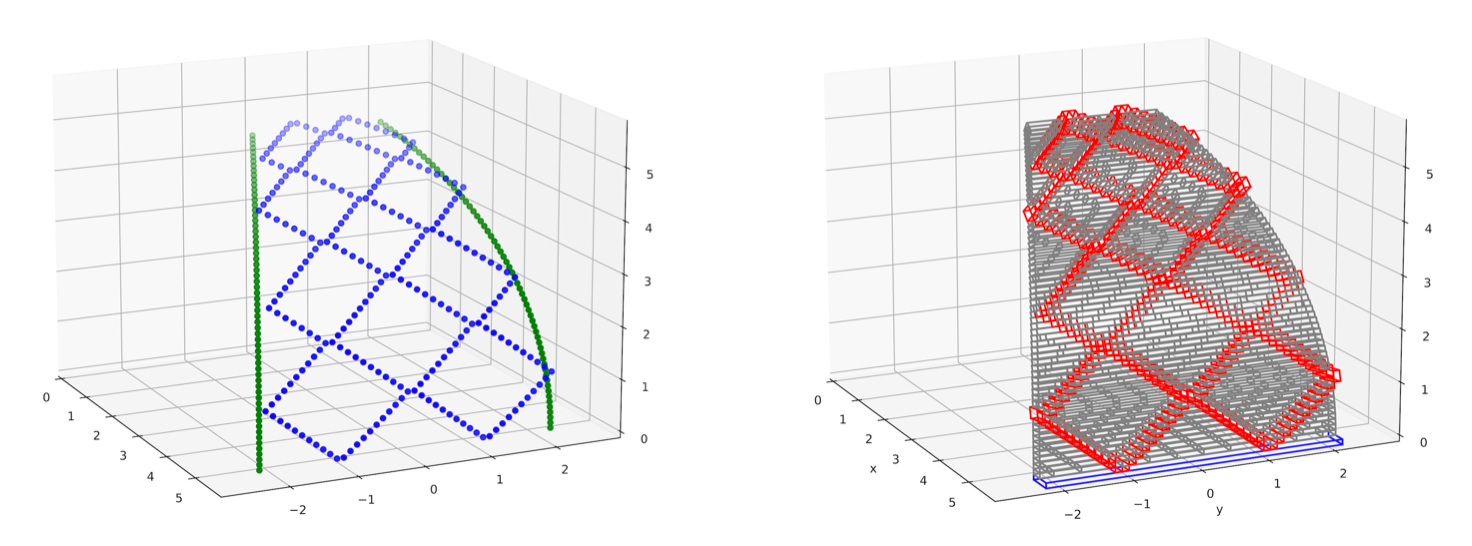
In order to compute the RBE and assess the double-helix pattern in different configurations, a parametric model of the dome is needed. To reduce the computational cost, the symmetries of the dome are exploited and only one dome section is modeled. First, the double-helix pattern is formulated mathematically and displayed in a 3d environment (left). With the boundaries defined, the dome section is filled with masonry bricks (right).

In order to create different variations of a double-helix masonry dome, some of the defining parameters are highlighted in the table below. The stretch factor defines whether the dome has a spherical curvature or if it has been stretched or compressed by some constant; the dome sections parameter defines the number of sides that make up the polygonial dome.

structure	name	stretch factor	dome sections
1	spherical dome	1	8
2	stretched dome	2	6
3	compressed dome	0.8	4

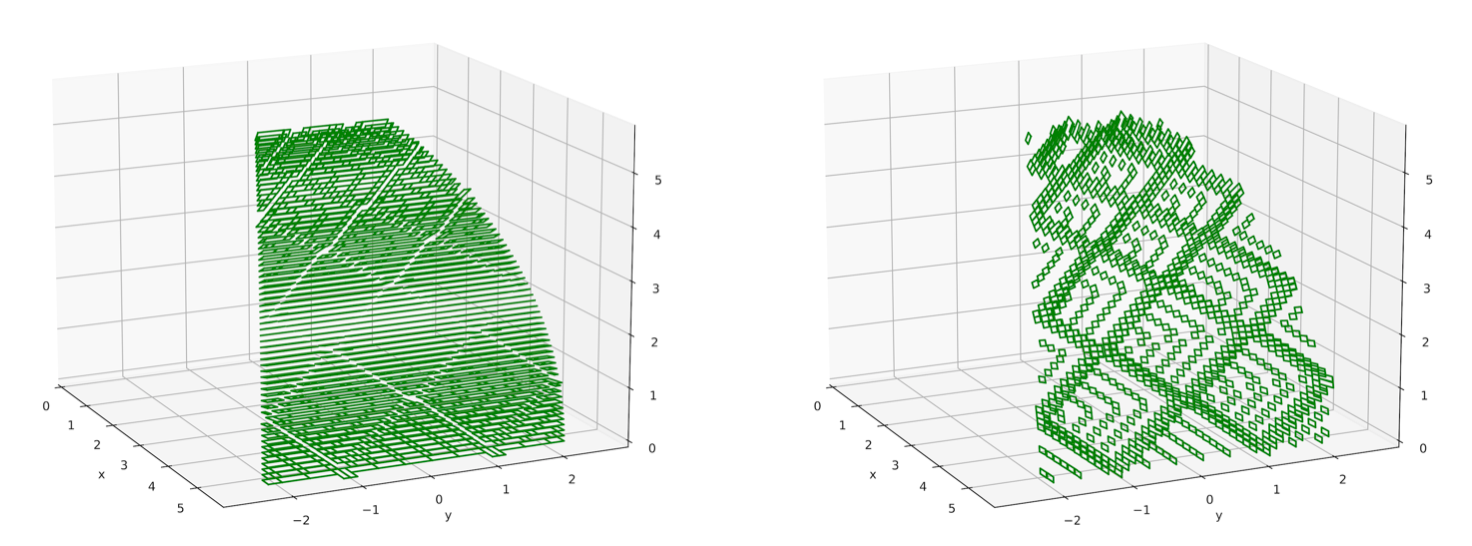
The dome section is now rotated around its own axis to model a complete dome model. The three structures translate into the parametric models that are displayed below in a Rhino environment. For each of these models, the double-helix pattern is configured uniquely, since it needs to match the geometries of the corresponding dome variant, defined by its parameters.

From here, the models are 3d printed in order to obtain physical prototypes of the masonry dome structures, as is shown on top of the post.

Rbe Computation and Internal Forces

The forces in the dome structure are transferred through the interfaces of the masonry bricks. Therefore, all interfaces that are present in the dome section are computed, where the horizontal (left) and vertical interfaces (right) are distinguished.

With a complete description of interfaces within the dome section, the RBE computation can commence. The equality constraints of the RBE are a linear system of equations that enforce the force and moment equilibrium for each brick. The static equilibrium of the entire masonry brick structure can be generalized in matrix form:

A_{e q} f + f_{e x t} = 0,

where $A_{eq}$ is the matrix of coefficients for the equilibrium equations and $f_{ext}$ are the external forces. The RBE is formulated as an optimization problem, where tension and isolated high forces are penalized as they typically lead to structural failure. Quadratic programming is used to find the optimal solution.

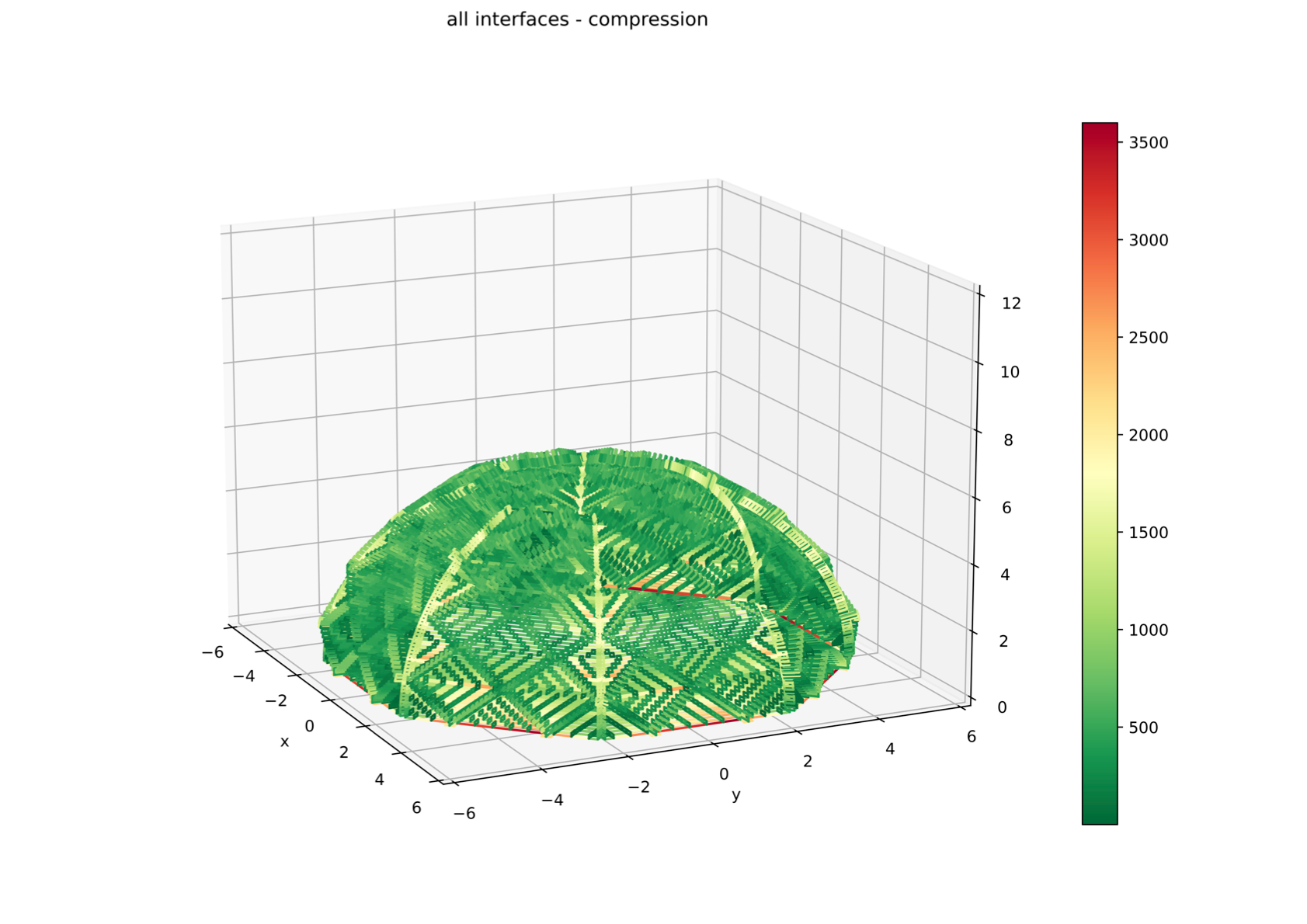
The computed solution of the internal compression forces of the brick interfaces for structure 1 is plotted, where the horizontal (left) and vertical (right) interfaces are distinguished.

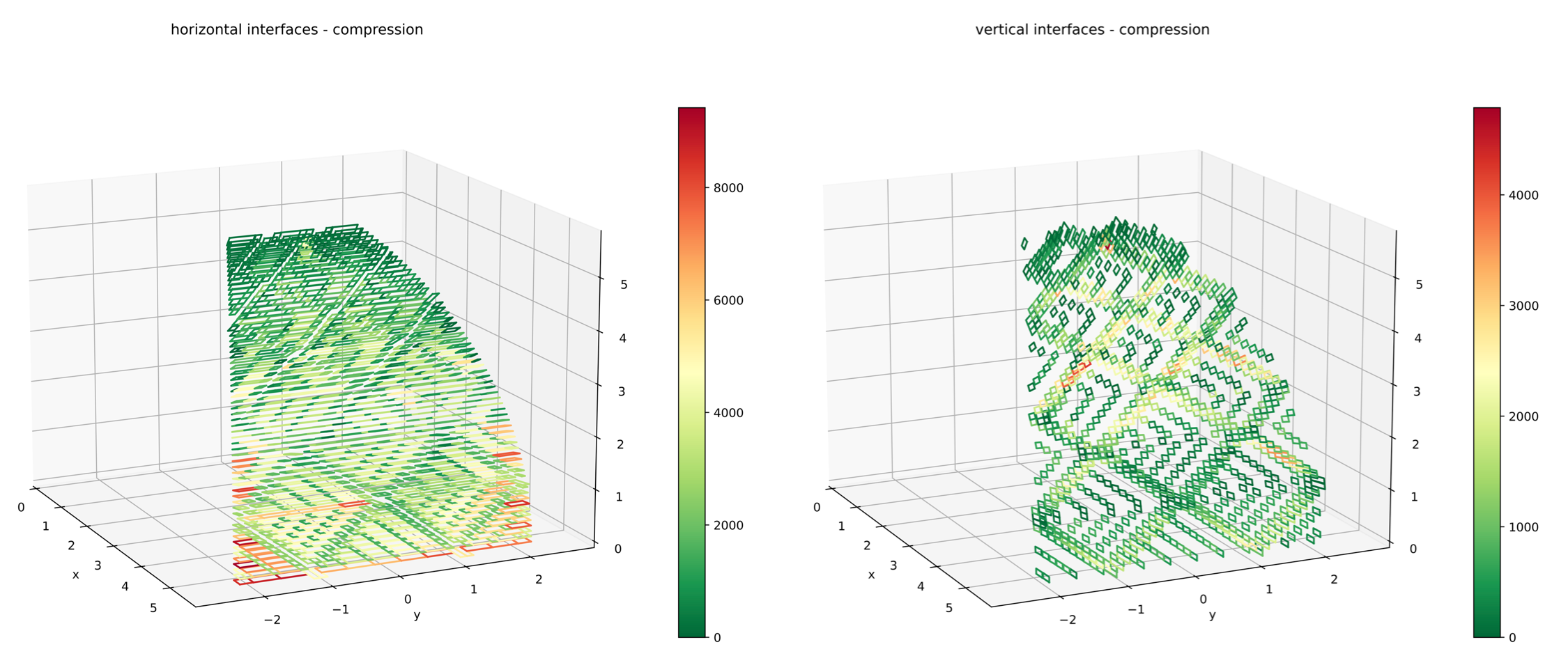
Especially the vertical interfaces show the impact of the double-helix pattern, guiding the force transmission through the structure. As done earlier, the symmetries of the dome are exploited to create a full compression forces plot of the double-helix masonry dome.

For a more detailed presentation of this thesis, see the full report.